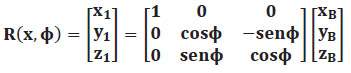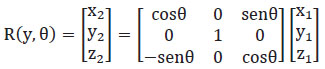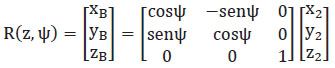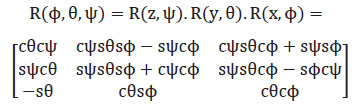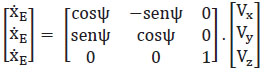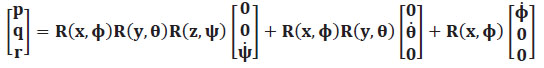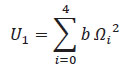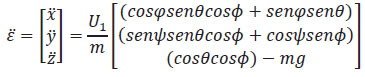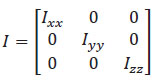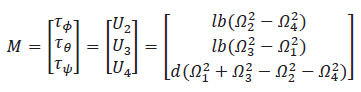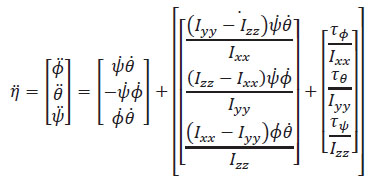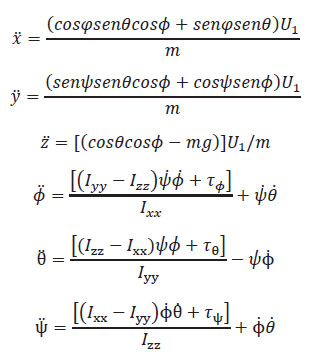INTRODUCCIÓN

En la actualidad y desde hace más de 50 años, el control y monitoreo de las diferentes actividades, con aparatos aéreos UAVs, se ha convertido en una área de gran interés. Hoy se realizan grandes esfuerzos [2], [3] en la generación de nuevos y mejores modelos matemáticos que rigen el funcionamiento para cumplir con diferentes tareas [5] como: control de incendios, contaminación de áreas, desplazamientos humanos, control de fronteras, tráfico de estupefacientes, control de fenómenos geológicos etc.

 

Movimientos del cuadricóptero

El cuadricóptero tiene cuatro rotores: frontal (1), lateral derecho (2), posterior (3) y lateral izquierdo (4), ver figura 1.1.

Los movimientos del cuadricóptero son de rotación y traslación, determinados a tres ejes fijos (X, Y, Z) y a través de la oscilación de los ángulos de navegación: yaw (eje Z); pitch (eje Y), y roll (eje X). El cuadricóptero tiene seis grados de libertad: tres traslacionales (x, y, z) y tres rotacionales (roll (), pitch () y yaw ()), ver Fig. 1.1.

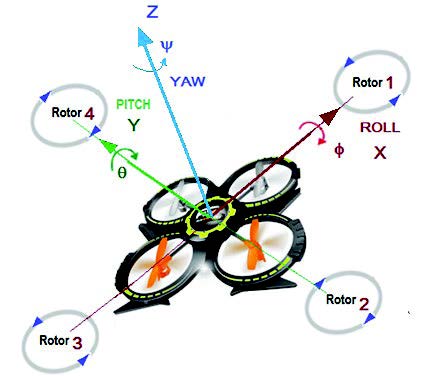
Figura 1.1. Esquema de Cuadricóptero

Fuente: Los autores 2020

Rotaciones Angulares

Rotacion Angular - ROLL

Rotación sobre el eje x, se obtiene al manipular las velocidades de los rotores 2 y 4, el par de rotores restantes permanece invariante en velocidad, al igual que el torque total. Se conoce como movimiento de Alabeo, hacia la izquierda y derecha.

 

Rotacion Angular - PITCH

Rotación sobre el eje y, se obtiene al modificar las velocidades de los rotores 1 y 3, el par de rotores restantes permanece invariante en velocidad, al igual que el torque total. Este es el movimiento de cabeceo Pitch, hacia adelante y atrás.

 

Rotacion Angular - YAW ()

Rotación sobre el eje z. Yaw Movimiento de Guiñada. La velocidad de los rotores 1 y 3 se aumenta, los rotores 2 y 4 se disminuyen para mover la orientación a la derecha, como se puede observar en la figura 1.1. Esto produce un desbalance aerodinámico de los torques que permite que el cuadricóptero gire en su propio eje. Si todos los rotores mantienen la misma velocidad, el torque total será cero; y si además el empuje total de la aeronave es igual a su peso, esta se mantendrá en vuelo estacionario.

 

Sistema de Referencia

Para obtener las ecuaciones de la dinámica del sistema, es necesario expresar diversas fuerzas y momentos en el sistema de referencia inercial. El cuadricóptero se mueve en el transcurso del tiempo, este cambia de posición respecto a un punto de referencia que se supone fijo. Son necesarios un sistema de referencia inercial y un segundo sistema de referencia no inercial. La posición del dron se referirá a través de dos puntos: uno fijo en tierra E={xE,yE, zE}, y el otro en el centro de masa del cuadricóptero B={xB, yB, zB},. La posición y traslación del cuadricóptero se describen mediante el movimiento de los ángulos Roll (), Pitch (), y Yaw (), ver fig. 1.2. En el sistema de referencia B se emplean las ecuaciones dinámicas de rotación y translación, este punto está en el centro del cuadricóptero y a él se refieren los giros y movimientos que realiza. (Raza, 2010).

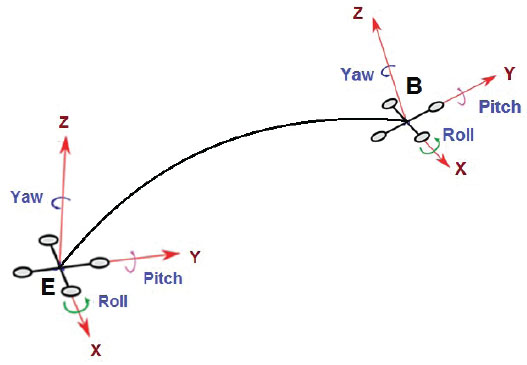
Figura 1.2. Sistema de Referencia

Fuente: Los autores 2020

La posición ᶓ del cuadricóptero en el punto E está determinado por el vector:

ᶓ = [ x y z ]^T, y la orientación por el vector ᶯ =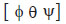

En función de estos ángulos 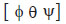se formula la orientación del dron con respecto al sistema de referencia E.

Para la matriz de rotación se usa la convención 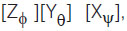movimiento alrededor de los ejes

 

Matriz Rotación en ROLL

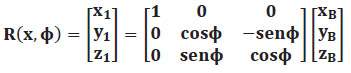
Ecuación 1.1. Matriz de rotación en ROLL

Matriz Rotación en PITCH

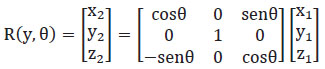
Ecuación 1.2. Matriz de rotación en PITCH

Matriz Rotación en YAW

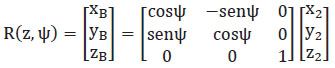
Ecuación 1.3. Matriz de rotación en YAW

Con las matrices de rotación de los ángulos se efectúa el cálculo de la matriz de rotación completa, Ecuación 1.4, la matriz R .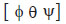

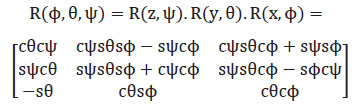
Ecuación 1.4. Matriz de rotación

Esta ecuación expresa el movimiento de traslación del cuadricóptero.

La matriz ecuación 1.4 se reduce cuando al considerar: los ángulos 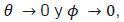entonces: es válida debido a que las rotaciones roll y pitch son bajas.

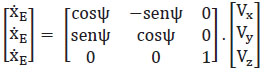
Ecuación 1.5. Modelo cinemático simplificado de un cuadricóptero

El vector [Vx Vy Vz] = V^T representa las velocidades del cuadricóptero en el sistema de referencia B y el vector 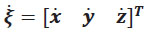representa las velocidades del cuadricóptero en los ejes x, y, z respectivamente. Para adquirir las velocidades en el punto de inercia se realiza el producto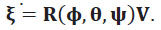

Para conseguir las ecuaciones de movimiento rotacional w del cuadricóptero, se emplean los componentes de las velocidades angulares roll (p), pitch (q) y yaw (r): El vector w = [ p q r ]^T , en el punto B. Las velocidades angulares w del cuadricóptero y la variación con respecto al tiempo de los ángulos 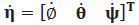en el punto E. La rotación yaw está sujeta a tres rotaciones en (z, y, x); Pitch está sujeta a dos rotaciones (y, x) y roll está sujeta a una rotación alrededor de x. (Espinosa Acosta & Moya González, 2016), (Artale, Milazzo, & Ricciardello, 2013) (Samaniego Villacres & Vaca Cerda, 2017)

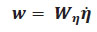
Entonces el valor de W_n

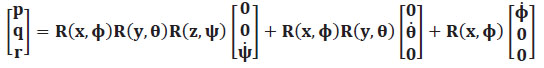
Las componentes de velocidades angulares en el eje x, y, z en el punto B:

Para conseguir 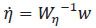se encuentra que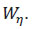

Ecuación 1.6. Modelo cinemático

Modelo Dinámico

En la formulación de las ecuaciones del modelo dinámico se van a asumir las siguientes hipótesis [1]:

1. Se considera al cuerpo central del dron como un sólido rígido libre 3D, por tanto tendrá 6 grados de libertad.
2. La inercia de los rotores respecto de sus ejes principales se considera despreciable.
3. La trayectoria del dron es muy pequeña comparada con el tamaño de la Tierra. Por ello se desprecian las fuerzas de
4. Coriolis y centrífuga.
5. La aceleración de la gravedad es constante, pues las variaciones de altura que va a experimentar el dron son despreciables frente al radio de la Tierra.
6. Se considera el efecto del viento en la resistencia aerodinámica del dron pero se desprecia el efecto en las hélices.
7. Se desprecian los momentos producidos por las fuerzas de resistencia aerodinámica, las fuerzas de arrastre aerodinámico actúan siempre en el centro de masas del sistema.

Al aplicar las ecuaciones de Newton Euler al cuadricóptero, se encuentran las ecuaciones que gobiernan el movimiento lineal y angular [7]. La fuerza que actúa sobre el cuadricóptero es:

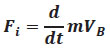
Ecuación 1.7. Fuerza sobre el cuadricóptero

Donde F es la fuerza que actúa sobre el dron, m la masa y esta se mantiene constante; VB la velocidad de traslación en el punto de referencia B.

La fuerza externa se constituye en: empuje de las hélices, fuerza gravitacional y la fuerza centrífuga. Debido al tamaño del dron, se desprecian los efectos o pares aerodinámicos. Cada motor i tiene una velocidad angular Ω_i, esta crea una fuerza referida al marco inercial del dron f_i=[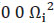], entonces el empuje total TB está representado como T_B=[0 0 U₁], donde U₁ es el empuje generado en el eje Z_B, como en la ecuación 1.8

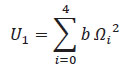
Empuje generado en el eje Z_B

Donde b es el factor de empuje generado por las hélices y su unidad es [N s² ]. El empuje total en conjunto con la fuerza de la aceleración de la gravedad representa la sumatoria de fuerzas totales que opera sobre el UAV como se indica ecuación 1.8, por tanto, el componente de traslación referido al sistema de referencia queda expresado como:

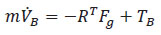
Ecuación 1.8. Componente de traslación

Para encontrar la fuerza con respecto al sistema inercial, se utiliza la ecuación: 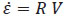y se la deriva para obtener 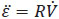considerando que la fuerza gravitacional está definida como 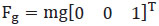, se obtiene el modelo dinámico de traslación:

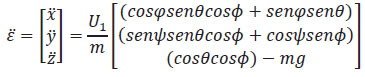
Ecuación 1.9. Modelo dinámico de traslación de un cuadricóptero

Para hallar el factor rotacional, el cuadricóptero posee una configuración simétrica con relación a los ejes x, y, z; por ello se desprecian los valores giroscópicos, la matriz de inercia I es:

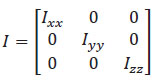
Ecuación 1.10. Matriz de inercia

Para hallar el momento total de I se considera los cambios del momento angular 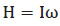, y se tiene que ecuación 1.11:

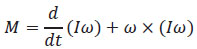
Ecuación 1.11. Momento que actúa sobre el cuadricóptero

El valor del momento total M, está determinado por las torques rotacionales generados por las hélices de los rotores y definidos como:

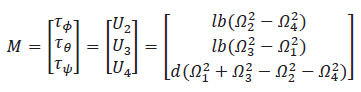
Ecuación 1.12. Momentos generados por las hélices

Donde l es la longitud del brazo hasta el centro de masa en unidades de metros y d el coeficiente de arrastre asociado a las hélices en unidades de [Ns² ].

Incluyendo las definiciones del modelo cinemático rotacional, los torques de las hélices, se presenta en ecuacion1.13 la dinámica que rige la rotación del cuadricóptero es:

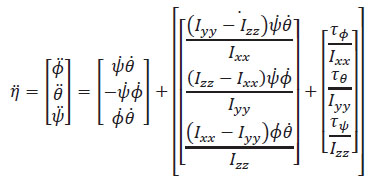
Ecuación 1.13. Modelo dinámico rotacional

El modelo dinámico completo de un cuadricóptero es:

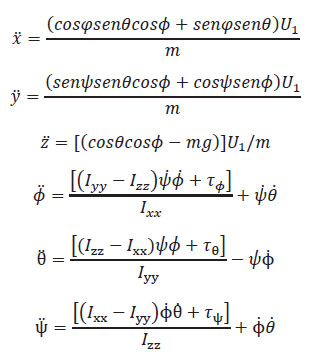
Ecuación 1.14. Modelo dinámico completo

Software de Control

Este proyecto plantea un marco de referencia completo para seguimiento de trayectoria, traslación y posicionamiento de un AR Drone que vuela en entornos abiertos. El sistema funciona de manera centralizada en un computador instalado en una estación terrestre.

El dron será controlado automáticamente, desde un computador. El desempeño del dron referido a través de los modelos: cinemático y dinámico y que en conjunto y con ayuda de un control no lineal PID [4], [5], ligado con un filtro de KALMAN [16], el dron trabajara en un medio con incertidumbres y no linealidades [6]. El filtro de Kalman está diseñado para estimar los estados del vehículo fusionando datos de posición, velocidad y aceleración. El controlador no lineal está diseñado en base a un modelo dinámico del AR Drone con la estabilidad de lazo cerrado probada usando la teoría de Lyapunov [19].

 

Actuación sobre el Dron en función de su posición y de la ruta programada ver figura 1.3.

Para controlar el DRON se lo hace a través de una estación de radiofrecuencia conectada al computador. Cada uno de los canales de comunicación del AR.Drone se lo controla independientemente desde el computador.

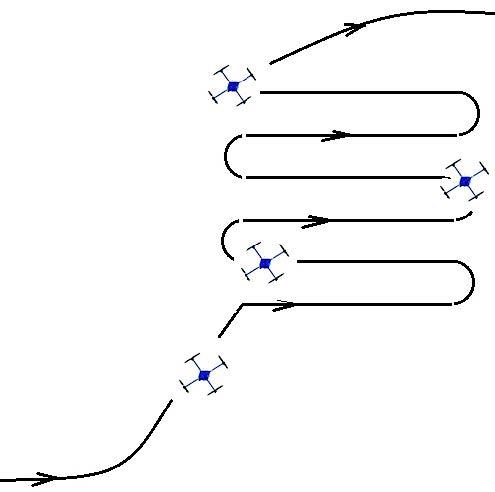
Figura 1.3. Trayectoria del Ar Drone

Fuente: Los autores 2020

El AR DRONE 2.0. Está compuesto por la unidad IMU: giroscopio, acelerómetro y magnetómetro de tres ejes, un sensor de presión que actúa como un altímetro.

Tecnología WIFI 802.11 b/g/n. Brújula 3D que permite controlar el vuelo con referencia absoluta y estimación dinámica del viento. Duración de la batería: 12 minutos. Tiene cuatro rotores con hélices de una longitud de 20 cm, sujeto a una sólida cruz de fibra de carbono que proporciona estabilidad.

 

El Parrot AR.Drone pesa 380g

La computadora a bordo se compone de un procesador ARM Cortex de 32 bits a 1 GHz, con un procesador digital de señal de 121 Gb de memoria RAM DDR2. [12].

 

Software del Parrot AR.Drone

El Parrot AR.Drone [12], [15], contiene todo el software a bordo requerido para hacer volar el cuadricóptero, este software no puede ser modificado externamente. La comunicación se lo realiza a través de protocolo telnet; además realiza internamente el control de los ángulos roll, pitch, la velocidad de yaw y la velocidad vertical.

Al conectar la batería del AR.Drone se activa una red WiFi ad-hoc, que permite el acceso a los canales de comunicación del drone, enviando datos y recibiendo comandos de navegación, de control.

• Canal de navegación (puerto UDP 5554), este canal envía la información de la orientación del drone en roll, pitch y yaw; los valores de velocidades lineales respecto a su sistema de referencia, la altura del drone y el estado de la batería y permite la recepción de los estados.
• Canal de video (puerto UDP 5555), en este canal se transmite de manera continua el video captado por las cámaras del drone.
• Canal de comando (puerto UDP 5556), en este canal se transmite la secuencia de paquetes de comandos que definen las referencias de la velocidad lineal horizontal, la velocidad de rotación en yaw y la velocidad vertical.

 

Visual Studio

Visual Studio es un conjunto de herramientas y otras tecnologías de desarrollo de software basado en componentes para crear aplicaciones eficaces y de alto rendimiento. Es un conjunto completo de herramientas de desarrollo para la generación de aplicaciones web, Servicios Web, aplicaciones de escritorio y aplicaciones móviles. Utiliza todo el entorno de desarrollo integrado, que habilita el uso compartido de herramientas y facilita la creación de soluciones en varios lenguajes.

Para el diseño del controlador tipo PID se utilizara el Software CV.Drone y se conecta a la red del AR.Drone.

Con el modelo de cuadricóptero definido en la ecuación 1.14; se describe la translación y rotación en yaw de un cuadricóptero se realizara el diseño de un controlador tipo PID, utilizando el análisis de estabilidad de Lyapunov.

 

FORTALEZA del ARDRONE 2.0.

Las bondades antes señaladas hacen de este dron, el vehículo adecuado para la aplicación de esta metodología y de posible manejo; canales de comunicación hacia la IMU, del dron, con ayuda del protocolo telnet es posible ingresar a modificar el control de los ángulos: roll, pitch y yaw, como también al velocidad y altura del dron.

Se realizaron pruebas de funcionamiento en ambiente abierto: el ARDRONE 2.0 funciona adecuadamente a temperaturas menores a los 10oC, presentando inconvenientes a temperaturas mayores a este valor; y ante la presencia de vientos fortuitos en la ciudad de Quito es errático y pierde fácilmente la ruta trazada, debido al poco peso de este dron 380 gramos.

 

Conclusiones

El Ardrone 2.0 tiene facilidades que el fabricante entrega al usuario, para realizar este tipo de investigaciones, como son, los canales de comunicación; no presente en otro tipo de dron.

Para el desempeño a ejecutar con este dron, una trayectoria predefinida y fija, resulta un tanto difícil mantenerla: Las variaciones de viento, temperatura, humedad relativa, que incrementan las no-linealidades e incertidumbres. Los tiempos de comunicación entre el dron y el sistema deben ser menores a 10-3 [s]; eso significa hardware de mejor desempeño y mayores costos.

Es necesario agregar un sistema de control de mayor robustez, quizá un Control en Modo deslizante, y filtros de Kalman, lo que obliga a realizar investigaciones más profundas dentro de laboratorios con mejor tecnología.
Para cumplir con los objetivos de este tipo de investigación, será necesario construir un dron: uno de mayor capacidad de tiempo de vuelo, mayor envergadura y peso, lo que significa, mayor presupuesto que el designado, para este trabajo. [13], [14].

 

Bibliografía

1. Agustín, C., & Bautista Soler, J. (2000). Física. Madrid: ANAYA.

2. (Espinosa Acosta & Moya González, 2016).

3. Barquín Murguía, A. I. (2014). Implementación de un Controlador externo en uncuadricóptero comercial. Ciudad de México: Universidad Autónoma de México.

4. Mazzone, V. (2002). Controladores PID Automatizacion y Control Industrial. Quilmes.

5. Rosero Paredes, L. E. (2014, Septiembre). Diseño y construcción de un módulo de Control PID para estabilización de un cuadricóptero. Quito: Escuela Politécnica Nacional.

6. Ornelas Tellez, F. (1994). Análisis de Sistemas No Lineales. Análisis de Estabilidad. Morelia México: Universidad San Andrés de Hidalgo

7. Raffo, G. (2007). Modelado y Control de un Cuadrator. Sevilla: Universidad de Sevilla.

8. Raza, S. A. (2010, January 01). http://cdn.intechopen.com/pdfs/6587/InTech-Intelligent_flight_control_of_an_autonomous_quadrotor.pdf. Retrieved Marzo 16, 2017.

9. Estrategias de control PID y basado en espacio nulo para una formación de cuadricópteros

10. 2013 IEEE International Conference on Robotics and Automation (ICRA) Karlsruhe, Germany, May 6-10, 2013.

11. Vargas Fonseca, L. M. (2015, Septiembre). Desarrollo de Algoritmos para seguimiento de trayectorias utilizando técnicas modernas de Control. Quito, Pichincha, Ecuador.

12. Parrot AR.Drone 2.0 Elite Edition,” Sitio Web Official de Parrot, 15-Nov-2017.[Online].Available:https://www.parrot.com/es/drones/parrot-ardrone-20-elite edition.

13. Jepherson, Jhon Blandon. (2016). Diseño de un dron para carga útil de 5kg. Universidad Tecnológica de Pereira. Colombia.

14. Rupérez, Pablo, JHON Blandon. (2014). Diseño y fabricación de un Dron. Universidad Politécnica de Valencia. España.

15. A. Hernandez, C. Copot, R. D. Keyser, T. Vlas, and I. Nascu, “Identification and path following control of an AR.Drone quadrotor,” in 2013 17th International Conference on System Theory, Control and Computing (ICSTCC), 2013.

16. Kalman and Extended Kalman Filters: Concept, Derivation and Properties,” ResearchGate. [Online]. Available: https://www.researchgate.net/publication/2888846_Kalman_and_Extended_Kalman_Filters_Concept_Derivation_and_Properties. [Accessed: 28-Mar-2018].

17. Yépez Rivera, M. (2013). Funciones de Lyapunov y algunas aplicaciones. México: Universidad de Veracuzana.

18. Astrom, K., & T., H. (2009). Control PID avanzado. Madrid España: Prentice Hall.

19. Vago, Santos, Sarcinelli-Filho, & Carelli, Estabilidad Lyapunov. 2014, págs. 756-767