INTRODUCCIÓN 

El procesamiento de imágenes está dentro de una de las áreas de la matemática aplicada que estudia la manipulación y análisis de elementos contenidos en una imagen digital mediante un procesador. Se lo puede definir como la agrupación de técnicas empleadas que tienen como finalidad mejorar su calidad, en el cual un sistema de análisis tiene un parámetro de entrada una imagen, y el resultado es otra imagen ya procesada. Tiene aplicaciones en áreas como la medicina, telecomunicaciones, agricultura, procesos industriales, satélites etc. (Bahamón Cortés, 2011) (Wang, Bovik, & Sheikh, 2004)

Las imágenes digitales están sujetas a una gran variedad de distorsiones durante la adquisición, el procesamiento, la compresión, el almacenamiento, la transmisión y la reproducción, cualquiera de los cuales puede provocar una degradación de la calidad visual. Las métricas de validación de la calidad de imagen son muy importantes para numerosas aplicaciones de procesamiento de imágenes. Para las aplicaciones en las que las imágenes deben ser vistas por los seres humanos, el único método "correcto" para cuantificar la calidad de la imagen visual es a través de una evaluación subjetiva. En la práctica, sin embargo, la evaluación subjetiva suele ser incómoda, lenta y costosa. El objetivo de la investigación en la evaluación objetiva de la calidad de imagen es evidenciar que existen medidas cuantitativas que puedan predecir automáticamente la calidad de imagen percibida. (Wang, Bovik, & Sheikh, 2004)

Una métrica objetiva de calidad de imagen puede desempeñar una variedad de funciones en las aplicaciones de procesamiento de imágenes. Las métricas de validación se pueden clasificar en compresión de imagen, segmentación, clasificación, agrupamiento, detección de bordes y extracción de características. (Ananthi, Balasubramaniam, & Kalaiselvi, 2016)

 

Justificación

En los últimos años se ha producido un crecimiento en las tecnologías del procesamiento de imágenes. El costo del procesamiento digital de alta capacidad se ha reducido considerablemente. Lo que ha provocado que cada vez sea mayor el número de imágenes que se obtienen para su caracterización. Por ejemplo, en la automatización agrícola, la tecnología de procesamiento de imágenes se utiliza para analizar enfermedades fúngicas en los cultivos, y un problema básico es extraer las manchas de enfermedades de las partes normales de las hojas de los cultivos. Otras aplicaciones incluyen procesamiento de imágenes médicas, recuperación de imágenes basadas en contenido, seguimiento de objetos, etc.

 

Desarrollo

Las medidas objetivas de calidad de imagen desempeñan papeles importantes en diversas aplicaciones de procesamiento de imágenes. Básicamente hay dos clases de enfoques de evaluación objetiva de calidad o distorsión. Las primeras son medidas definidas matemáticamente, como el error cuadrático medio (MSE) ampliamente utilizado, la proporción máxima de señal-ruido (PSNR), la raíz del error cuadrático medio (RMSE), el error absoluto medio (MAE) y la relación señal-ruido (SNR). La segunda clase de métodos de medición considera las características del sistema visual humano (HVS) en un intento de incorporar medidas de calidad perceptiva. (Pappas & Hill, 2000)

La métrica de calidad de referencia completa más simple y más utilizada es el MSE, que se calcula promediando las diferencias de intensidad cuadrada de los píxeles de imagen distorsionados y de referencia, junto con la cantidad relacionada de la PSNR. Son atractivos porque son fáciles de calcular, tienen significados físicos claros y son matemáticamente convenientes en el contexto de la optimización. Pero no coinciden muy bien con la calidad visual percibida. En las últimas tres décadas, se ha realizado un gran esfuerzo para desarrollar métodos de evaluación de calidad que aprovechen las características conocidas del HVS. La mayoría de los modelos de evaluación de calidad perceptual propuestos han seguido una estrategia de modificación de la medida MSE para que los errores sean penalizados de acuerdo con su visibilidad. (Wang & Bovik, 2002)

En este documento se presentan las métricas de validación, las cuales se clasifican en cinco áreas principales en las aplicaciones de procesamiento de imágenes.

 

Compresión de imágenes

La compresión de imágenes minimiza el tamaño en bytes de un archivo de gráficos sin degradar la calidad de la imagen a un nivel inaceptable. La reducción en el tamaño del archivo permite almacenar más imágenes en una cantidad determinada de espacio en disco o memoria. (Jaya & Gopikakumari, 2013)

Relación de compresión: La relación de compresión se define como la relación entre el tamaño de la imagen original y el tamaño de la imagen comprimida y se define a continuación:

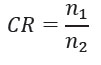
Donde n₁ y n₂ representan el número de bits requeridos para la imagen original y comprimida respectivamente.

Proporción máxima de señal-ruido (PSNR): El PSNR se usa más comúnmente para medir la calidad de la reconstrucción de códecs de compresión con pérdida. (Kalaiselvi et al., 2017). La señal en este caso son los datos originales, y el ruido es el error introducido por la compresión. Al comparar códecs de compresión, PSNR es una aproximación a la percepción humana de la calidad de la reconstrucción. El PSNR es la relación entre la potencia máxima posible de una señal y la potencia del ruido corruptor que afecta la fidelidad de su MSE. El PSNR (en db) se define como:

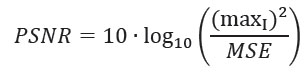
Donde maxI es la fluctuación máxima en una imagen.

Error cuadrático medio (MSE): PSNR se define más fácilmente a través del error cuadrático medio (MSE) y se define como:

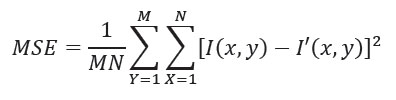
Donde, I (x,y) es la imagen original, I'(x,y) es la versión aproximada (que en realidad es la imagen descomprimida) y M,N son las dimensiones de la imagen. Lógicamente, un valor más alto de PSNR es bueno porque significa que la relación de señal a ruido es más alta. (Kalaiselvi, 2016)

 

Segmentación

Considerando que la segmentación es un tema importante en muchas aplicaciones basadas en imágenes. Este proceso, implica segmentar una imagen en varias partes disjuntas, cada una de las cuales contiene un objeto de interés. Por ejemplo, en la automatización agrícola, la tecnología de procesamiento de imágenes se utiliza para analizar enfermedades fúngicas en los cultivos, y un problema básico es extraer las manchas de enfermedades de las partes normales de las hojas de los cultivos. Otras aplicaciones incluyen procesamiento de imágenes médicas, recuperación de imágenes basadas en contenido, seguimiento de objetos, etc. (Jia & Zhang, 2008)

Las métricas de evaluación se utilizan popularmente para acceder al rendimiento de los resultados del algoritmo de segmentación (Ananthi, Balasubramaniam, & Kalaiselvi, 2015), las cuales se presentan a continuación:

 

Coeficiente de Jaccard

El coeficiente de similitud de Jaccard es una estadística utilizada para comparar la similitud de dos imágenes y se define como el tamaño de la intersección dividido por el tamaño de la unión de las imágenes.

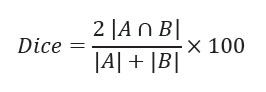
Donde A y B son dos imágenes. Si el valor del coeficiente es 1, entonces muestra la alta similitud entre A y B. De lo contrario, si su valor es 0, entonces no hay similitud entre A y B.

Precisión

Calcula el porcentaje de predicción positiva realizada por los clasificadores que son correctos.

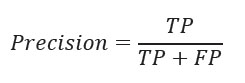
Donde TP es el número de clases positivas correctamente clasificadas como positivas y FP es el número de clases negativas clasificadas incorrectamente como positivas.

Recall

Calcula el porcentaje de patrones positivos que el clasificador detecta correctamente.

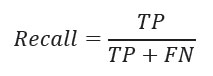
Donde TN es el número de clases positivas clasificadas incorrectamente como negativas y FN es el número de clases negativas clasificadas correctamente como negativas.

 

Clasificación

El sistema visual humano (HVS) es otro enfoque para medir la calidad de la imagen. El HVS es un método que utiliza el ojo humano como referencia. La idea principal es que los humanos están interesados en diferentes atributos de la imagen además de tomarla como un todo. Estos atributos incluyen brillo, contraste, textura, orientación, etc. (Gil, 2011). Se han desarrollado muchos tipos diferentes de modelos HVS para medir la calidad de la imagen, sin embargo, entre todas las medidas objetivas, la medida HVS se considera la más cercana a las medidas subjetivas. A continuación, se enumeran dos métricas basadas en el sistema visual humano.

• Índice de calidad de imagen universal - Universal Image Quality Index (UIQI)
• índice de similitude structural - Structural Similarity Index (SSIM)
  

 

Universal Image Quality Index (UIQI): El Índice de calidad de imagen universal fue propuesto por (Wang & Bovik, 2002), divide la comparación entre imagen original y distorsionada en tres comparaciones: luminancia, contraste y comparaciones estructurales como en las ecuaciones:

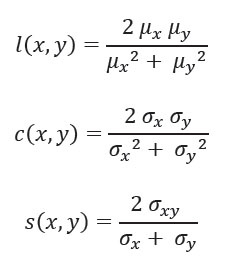
Donde μ_x μ_y denota los valores medios de las imágenes originales y distorsionadas. Y 𝜎𝑥 𝜎𝑦 denota la desviación estándar de las imágenes originales y distorsionadas, y 𝜎_𝑥𝑦 es la covarianza de ambas imágenes. Basado en las tres comparaciones anteriores, el UIQI se da:

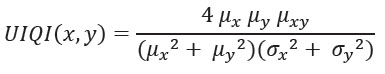
UIQI es una medida simple que solo cuenta con estadísticas de primer y segundo orden de las imágenes originales y distorsionadas. UIQI se considera una medida inestable y no se correlaciona con la evaluación subjetiva, por eso Wang & Bovik, propusieron la métrica del índice de similitud estructural.

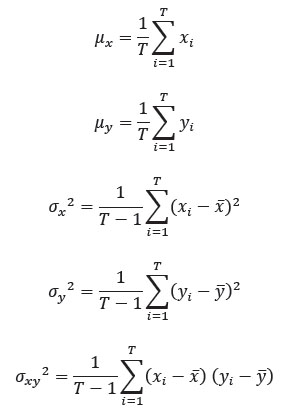
Structural Similarity Index (SSIM): (Wang & Bovik, 2002), propusieron el índice de similitud estructural como una mejora para UIQI. El índice medio de similitud estructural se calcula de la siguiente manera: en primer lugar, las imágenes originales y distorsionadas se dividen en bloques de tamaño 8 x 8 y luego los bloques se convierten en vectores. En segundo lugar, se calculan dos medias y dos derivaciones estándar y un valor de covarianza a partir de las imágenes como se muestra a continuación:

Tercero, las comparaciones de luminancia, contraste y estructura basadas en valores estadísticos se calculan como en UIQI, la medida del índice de similitud estructural entre las imágenes x e y viene dada por:

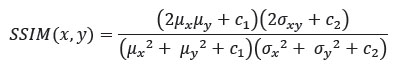
Donde, c₁ y c₂ son constantes. Al igual que en UIQI, SSIM se aplica localmente usando una ventana deslizante de tamaño B x B que se mueve píxel por píxel horizontal y verticalmente cubriendo todas las filas y columnas de la imagen, comenzando desde la esquina superior izquierda de la imagen. La calidad de imagen general MSSIM (Bhola, Sharma, & Bhatnagar, 2014) se obtiene calculando la media de los valores SSIM como:

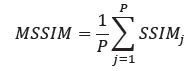
Donde, p es el número de ventanas deslizantes. UIQI y SSIM son más precisos y consistentes que MSE y PSNR a pesar de que cuestan más.

No hay duda de que un modelado más preciso del HVS siempre es ventajoso en el diseño de métricas de calidad de imagen. Sin embargo, sin un marco matemático bien definido, los esfuerzos en el modelado HVS no resultarán en una medida de calidad exitosa. Por ejemplo, la suma de errores en forma de la métrica de Minkowski.

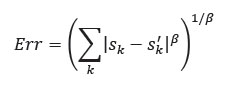
O su equivalente ha sido ampliamente adoptado por la mayoría de los modelos anteriores de evaluación de calidad de imagen y video, donde 𝛽  es una constante con un valor entre 1 y 4, y son los componentes de imagen correspondientes (en varios formatos, como valor de píxel, y coeficiente wavelet ponderado) de las imágenes originales y de prueba, respectivamente. Ésta no es una forma matemática apropiada para la evaluación de la calidad de imagen, ya que la diferenciación de imagen no captura de manera adecuada una estimación de la correlación entre s_k y s´_k, pero la idea presentada, es un punto de partida para el desarrollo futuros de métodos de evaluación de calidad de imagen. (Wang & Bovik, 2002)

 

Conclusiones

En este documento se ha discutido los detalles de varias métricas en referencia al procesamiento de imágenes digitales. En el campo del procesamiento de imágenes, la evaluación de la calidad de imagen es un problema fundamental y desafiante con muchos intereses en una variedad de aplicaciones, como el monitoreo dinámico y el ajuste de la calidad de imagen, la optimización de algoritmos y la configuración de parámetros de los sistemas de procesamiento de imágenes, y la evaluación comparativa del sistema de procesamiento de imágenes y algoritmos.

Los métodos convencionales PSNR y MSE no siempre concuerdan con los resultados de visualización subjetivos en caso de distorsión aditiva. El SSIM ofrece una buena precisión de evaluación y una formulación matemática simple.

Éste trabajo es un punto de inicio para futuras investigaciones con respecto al campo del procesamiento de imágenes.

REFERENCIAS BIBLIOGRÁFICAS

Ananthi, V., Balasubramaniam, P., & Kalaiselvi, T. (2016). A new fuzzy clustering algorithm for the segmentation of brain tumor. Soft Computing, 4859–4879.

Bhola, V. K., Sharma, T., & Bhatnagar, J. (2014). Image Quality Assessment Techniques 1, 161(May), 156–161.

Gil, J. (2011). Evaluación de calidad en la segmentación de imágenes, (ISSN 2072-6287).

Jaya, V. ., & Gopikakumari, R. (2013). IEM: A New Image Enhancement Metric for Contrast and Sharpness Measurements. International Journal of Computer Applications, 79(9), 1–9. https://doi.org/10.5120/13766-1620

Jia, Y., & Zhang, C. (2008). Learning distance metric for semi-supervised image segmentation, 3204–3207.

Kalaiselvi, T. (2016). ROI Based Hybrid Compression Techniques for Transferring MRI Brain Images, 4(4), 270–277.

Kalaiselvi, T., Vasanthi, R., & Sriramakrishnan, P. (2017). A Study on Validation Metrics of Digital Image Processing, (January).

Pappas, T. N., & Hill, M. (2000). Perceptual Criteria for Image Quality Evaluation. Handbook of Image and Video Processing, (908).

Wang, Z., & Bovik, A. C. (2002). A universal image quality index. IEEE Signal Processing Letters, XX, 2–5.

Wang, Z., Bovik, A. C., Sheikh, H. R., Member, S., Simoncelli, E. P., & Member, S. (2004). Image Quality Assessment : From Error Visibility to Structural Similarity, 13(4), 600–612.